Skip to main content

Section 3.6 Epilogue: word hyperbolic groups.

We started out this course with a rigorous construction of \(F(X)\) the free group on \(X\) which led to group presentations: a unified way of working with finitely presented groups. Immediately, it became apparent that a group doesn't have a distinguished generating set, nor a distinguished, finite, collection of relations. That is to say, a group presentation \(\pres X R\) is not determined by the (isomorphism class) of the group \(G\text{,}\) or in other words, presentations are not canonical. What would be canonical for finitely presented group \(G\) would be the infinite set of all finite presentation of \(G\text{,}\) which we described using Tietze transformations.

We ended the first chapter with Dehn's algorithmic problems:

  1. The word problem.
  2. The conjugacy problem.
  3. The isomorphisms problem.

All three of these problems are undecidable in general. This, combined with the fact that a group generally has no distinguished presentations, reinforce the conception that group presentations are completely useless. We ended the first chapter by trying to temper this impression by showing that when we restrict to a class of groups, in this case to the class of finitely generated free groups, we are able to solve all three of these algorithmic problems.

At the end of the first chapter we also presented an invariant, namely the first Betti number. We say it is an invariant because, unlike some presentation, it is determined by the isomorphism class of a group \(G\text{.}\) The second chapter was devoted to presenting the concept of quasi-isometry, which we motivated as follows: all finite generating sets of a group \(G\) are equally valid, and can give rise to different Cayley graphs. These Cayley graphs can look very different, but they are all going to be quasi-isometric. This leads us to consider spaces up to quasi isometry.

If we consider a finitely generated group \(G\) equipped with a word metric and forget about everything else this is nothing more than some countable set \(G\) with some function distance function \(d:G \times G \to \ZZ_{\geq 0}\text{.}\) Topologically, these are all just countable discrete sets, i.e. they are boring. It is only when considering such spaces up to quasi-isometry that they become interesting. For example we show that as metric spaces, \(\ZZ^2\) and \(\ZZ\) are not quasi-isometric.

Any group invariant will only give partial information about the group. The rest of chapter 2 is devoted to exploring the limitations of quasi-isometry and as a consequence of the Svarc-Milnor lemma it is shown that at best quasi-isometry can distinguish groups up to virtual isomorphism. An accurate analogy is that quasi-isometry is like a special pair of goggles: it lets you see entire groups, but your vision is blurry so some things you can tell apart like \(\ZZ\) and \(\ZZ^2\text{,}\) but other groups are indistinguishable, like \(\ZZ\) and \(\ZZ\oplus(\ZZ/2\ZZ)\text{.}\)

We ended Chapter 2 by showing that if we are only given a word metric on a group

\begin{equation*} d:G \times G \to \ZZ_{\geq 0} \end{equation*}

and the assurance that this metric space is quasi-isometric to \(\ZZ\text{,}\) then \(G\) is itself is virtually isomorphic to \(\ZZ\text{,}\) so that quite a bit of algebraic structure can be inferred from this purely metric information.

Chapter 3 is about actually calulating things. It starts by soliving yet another algorithmic problem within the class of free groups: the subgroup membership problem and introduces the concept of folding. We then introduce 2-complexes and van Kampen diagrams, which give us a geometric tool to study words representing the identity in a group presentation \(\pres X R\text{.}\) The concept of folding is used here because it is what enables us to construct a van Kampen diagram from a product of conjugates of relations.

Van Kampen diagrams allow us to use 2 dimensional topological arguments regarding groups. In particular, using tracks, we were able to prove fundamental results about HNN extensions and by using commbinatorial analogues of curvature we were able to show that Dehn's algorithm, a greedy approach to solving the word problem given a group presentation \(\pres XR\text{,}\) will almost surely work correctly provided the relations are chosen at random with length much longer than the number of relations.

In particular the \(C'(1/6)\) small cancellation condition is "generic", but it depends on a particular choice of presentation. Given a \(C'(1/6)\text{,}\) it is easy to ransform it using Tietze transformations so that it no longer satisfies the criteron. Also, how does this condition play with quasi-isometry?

Subsection 3.6.1 Isoperimetric inequalites and word hyperbolicity

Given \(G=\pres X R\) and some word \(w =_G 1\) we can define

\begin{equation*} \mathrm{area}(w) = \min\left(\left\{n \in \ZZ_{\geq 0} \middle|w = \prod_{i=1}^n a_ir_i^{\epsilon_i}a_i^{-1}\ \right\}\right) \end{equation*}

or, equivalently, the minimal number of \(R\)-2-cells among all van Kampen diagrams witnessing the triviality of \(w\) in \(\pres X R\text{.}\) Now given, \(\pres X R\) we can define the isoperimetric function of the presentation as the following :

\begin{align*} f_{\pres X R} :\ZZ_{\geq 0} \amp \to \ZZ_{\geq 0}\\ f(n)\amp= \min\left(\left\{\mathrm{area}(w) \in \ZZ_{\geq 0}\middle | |w|\leq n \right\}\right). \end{align*}

Clearly such functions are nonnegative and non-decreasing.

We say a presentation \(\pres X R\) is a Dehn presentation if Dehn's algorithm correctly solves the word problem. Recall that would take a \(C'(1/6)\) presentation and, while preserving the generating set, change the relations so that Dehn's algorithm no longer works.

We will now return to geometry. Let \(x,y,z\) be three points in a geodesic metric space (i.e. for any two points there is a path joining them realizing the distance), a geodesic triangle \(\Delta(x,y,z)\) is a union of three geodesics, one from \(x\) to \(y\text{,}\) one from \(y\) to \(z\text{,}\) and one from \(z\) to \(x\text{.}\) Note that in a graph, unlike in Euclidean space, there may by multiple geodesics joining two points. (See Figure 3.6.1.)

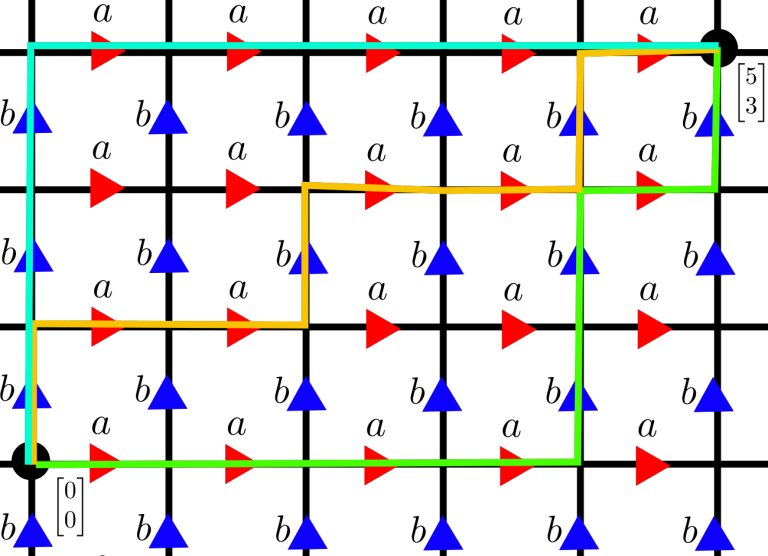
Figure 3.6.1. Three distinct geodesics joining \(\BEmatrix{0\\0}\) and \(\BEmatrix{5\\3}\) in \(\cay{\left\{\BEmatrix{1\\0},\BEmatrix{0\\1}\right\}}{\ZZ^2}\)

We say a geodesic triangle is \(\delta\)-thin if every side is contained in the union of the \(\delta\)-neighbourhood of the two other sides (see figure Figure 3.6.2.)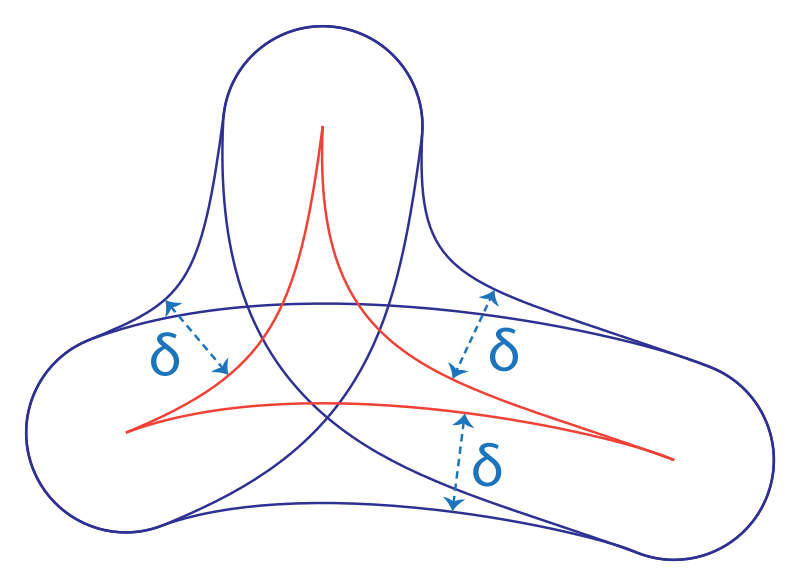

Figure 3.6.2. A \(\delta\)-thin triangle. Each side stays \(\delta\)-close to the union of the other two sides.

Recall that a geodesic metric space \(X\) is a space such that for any pair of points \(x,y \in X\) there is a path joining these points realizing this distance. A geodesic space is said to be Gromov hyperbolic if there exists a uniform \(\delta\) such that every geodesic triangle is \(\delta\)-thin. If \(X\) is a tree for example, then every geodesic triangle is a "tripod" so every side is contained in the 0-neighbourhood of union of the other two sides.

This notion of hyperbolicity plays well with quasi-isometry, in fact it is easy to show the following:

If \(X\) is Gromov hyperbolic and is quasi-isometric to \(Y\) then \(Y\) is also Gromov hyperbolic, though possibly with a different \(\delta\)-parameter.

As far as group theory is concerned we have the following equivalent characteristics.

We first note that this theorem says something about a group and not specifically about some presentation of the group. We will say that \(G\) is word hyperbolic if it satisfies any of the equivalent conditions of this theorem. A proof of this result (and much more) can be found in [2], which should now be understandable after doing this course.

We note that an argument using Tietze transformations and van Kampen diagrams immediately tell us that \(2. \Rightarrow 3.\) We will now make a few remarks about how \(1. \Rightarrow 2.\) is proved.

Subsection 3.6.2 A local to global property of Gromov hyperbolic spaces.

In normal differential geometry, shortest paths tend to be "straight lines". For example if \(p,q\) are two points in \(\RR^2\) equipped with the Euclidean geometry, then any path \(t \mapsto (x(t),y(t))\) joining \(p\) and \(q\) will be a shortest path if and only if the velocity \((x'(t),y'(t))\) is always parallel to the acceleration \((x''(t),y''(t))\text{.}\) In other words, and this is how it is classically, geodesics are defined via local properties: if a path looks "straight" at every point, then it is globally straight.

Now figure Figure 3.6.1 shows that in some geodesic metric spaces, we can have multiple geodesics joining two points, and furthermore, looking at a path locally doesn't tell us anything about its large scale behaviour. For example a path in a graph could close up on itself, but there will be no indication of this looking at edges and vertices individually. A consequence of Gromov-hyperbolicity is that there is some way to pass from local to global. Consider this "medium scale" local to global result:

To grasp the significance of this result. Note that this property is not enjoyed by the standard Cayley graph of \(\ZZ^2\) as shown in Figure 3.6.5, in fact for any \(k\) it is possible to construct arbitrarily long closed loops (so definitely not quasi-geodesics with reasonable constants) in this Cayley graph that are \(k\)-local geodesics.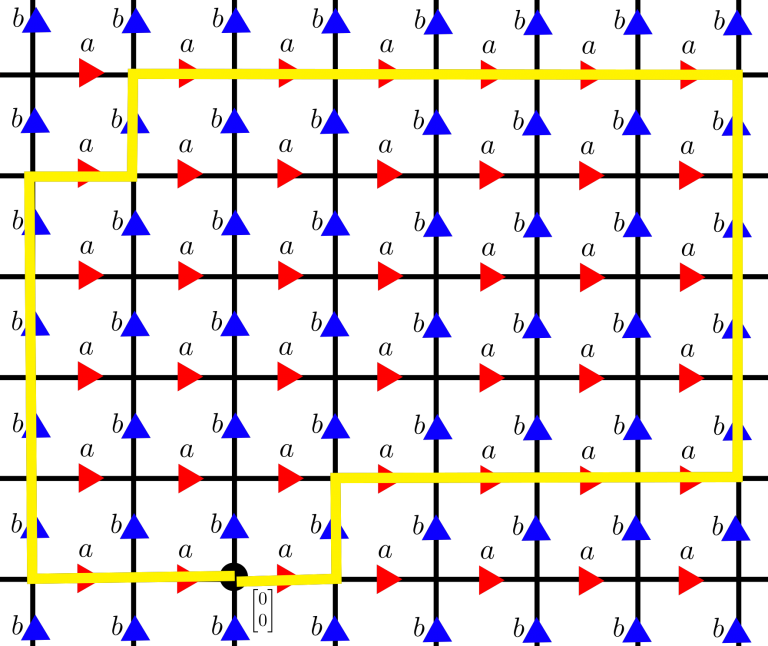

Figure 3.6.5. A \(4\)-local geodesic in \(\cay{\left\{\BEmatrix{1\\0}, \BEmatrix{0\\1}\right\}}{\ZZ^2}\) which is definitely not geodesic.

This leads to Dehn presenations as follows: an word \(w\) in some generating set \(\gen S = G\) is the label of some path \(\gamma_w\)in the Cayley graph, which is \(\delta\)-hyperbolic. Any word representing the identity is the label of a closed loop.

If all subwords of length \(8\delta+1\) of \(w\) are geodesic, this forces \(\gamma_w\) to be quasi-geodesic and since we know the parametrs, if \(w\) is sufficiently long its endpoints will be far from one another, so \(w\) cannot be a closed loop and therfore is not trivial. It follows that words representing the identity are either short (one of the finitely many words representing the identity of length at most some bound \(M\)) or long, but containing a subword of length at most \(8\delta+1\) that is not "geodesic". In the latter case, such subwords can pre replaced by a shorter words, decreasing the length of \(w\text{.}\) Repeating this gives Dehn's algorithm.

In fact this local to global property is more than just a consequence of Gromov hyperbolicity. For groups, possessing this property is in fact equivalent to hyperbolicity! This is just one reason why the class of hyperbolic groups is remarkable.

Subsection 3.6.3 Dehn's algorithmic problems in hyperbolic groups

The solution to all three of Dehn's algorithmic problems in hyperbolic groups has been a major achievement of geometric group theory. The solution to the word problem follows from Dehn presentations. A solution to the conjugacy problem (given \(g,h\) decide if there is some \(x\) such that \(xgx^{-1}h^{-1}=1\)) actually follows from \(\delta\)-hyperbolicity and a study of geodesic quadrilaterals.

The isomorphism problem for hyperbolic groups involved work spanning from 1995 to 2011. There is no simple way to explain how it works as it involves asymptotic methods to create exotic topological spaces arising from limits of spaces and canonical group decomposition theories. In other words, it's super cool!

Finally, it is worth pointing out that not every hyerpbolic group \(G\) admits a \(C'(1/6)\) presentation, even though they all admit Dehn presentations. The proof goes like this: there exist hyperbolic groups which satisfy something called Kazhdan's property (T), but it was also shown that \(C'(1/6)\) groups never satisfy this property. Once again, the proofs of these facts involve fascinating math.