An introduction to combinatorial and geometric group theory

Subsection 3.2.1 HNN extensions

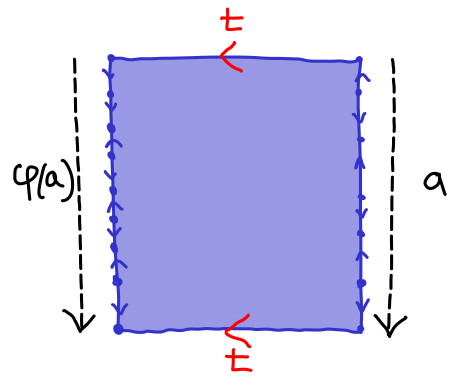
HNN extensions are named after mathematicians Higman, Neumann, and Neumann (the Neumanns were married.) They are formed by putting a group \(G\) inside a larger group \(G*_t\) with an extra generator called the stable letter, typically we use \(t\text{,}\) which conjugates elements in \(G\text{.}\) More precisely, suppose that \(G\) contains two subgroups \(A,A'\) such that \(A\approx A'\text{,}\) i.e. \(A,A'\) are isomorphic and let \(\varphi:A\stackrel{\sim}{\to} A'\) be a specific isomorphism. See Figure 3.2.1.

i.e. we add a new generator \(t\) (we assume \(t \not\in X\)), the stable letter, and for each \(a \in A\) we add a relation which says that conjugation of an element of \(a\) by \(t\) produces the same result as making taking the image \(\varphi(a)\text{.}\) Incidentally we slightly changed the convention for relations: instead of writing \(t^{-1}at(\varphi(a)^{-1}\) we wrote \(t^{-1}at = \varphi(a)\text{,}\) which is equivalent. Also note that for these relations we actually mean that we wrote words in \(X^{\pm 1}\) represeting elements in \(a,\varphi(a)\in G\text{.}\) In particular we are not assuming \(A,A'\subset X\text{.}\)

Needless to say, adding extra relations to a group can have unexpected consequences. We want to show that \(G \leq G*_t\text{,}\) i.e. that \(G*_t\) is an extension of \(G\text{.}\) Note that by Lemma Lemma 1.6.1 there is a natural homomorphism \(G \into G*_t\text{.}\) Our first task is to show that this homomorphism is injective.

Subsection 3.2.2 Dual tracks and van Kampen diagrams

Comapring the presentation \(G=\pres X R\) and the presentation given in (3.2.1) we see that we have extra HNN relations which give rise to the following 2-cells:

Within each such 2-cell, we can draw a dual \(t\)-track which a segment in each HNN-2-cell joining the midpoints of the \(t\)-labeled edges. Within a van Kampen diagram, because the only place \(t\)-labelled edges occur is either as fully external edges, or inside HNN-2-cells, these segments join up to make dual \(t\)-tracks in van Kampen diagrams.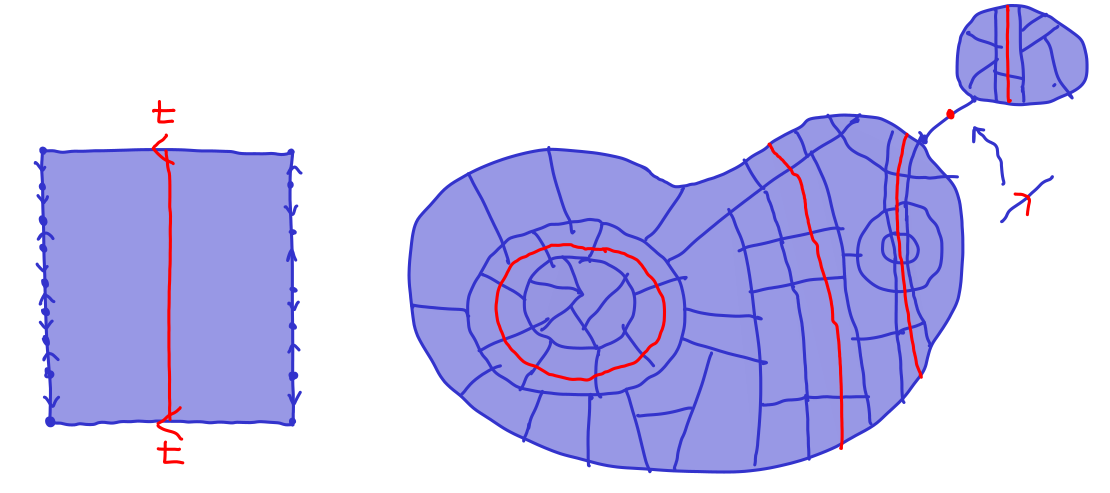

This next lemma is a topological consequence of our requirements that van Kampen diagrams are planar and simply connected, that dual tracks are curves, and the Jordan curve theorem. One could probably also come up with a simpler purely combinatorial proof... but whatever, the lemma is completely obvious.

We note that if a point type or an arc type track did not divide \(\mathcal D\) into two distinct components we would violate simple connectivity. If a circular track did not divide into two components we would have an embedded Möbius strip.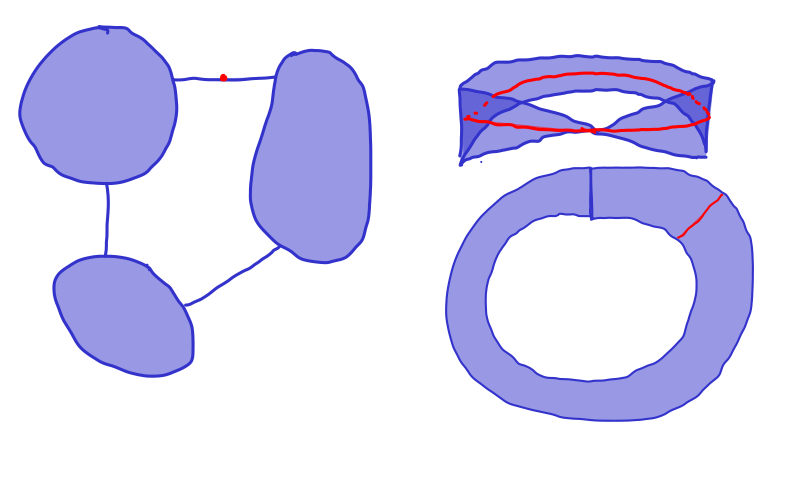

This topologically flavoured lemma is the key to proving things about HNN extensions. We start with the following:

Consider the two presentation. The inclusions \(X \into X\cup\{t\}\) and \(R \into R \cup\{t^{-1}w_at(w_{\varphi(a)})^{-1}\mid a \in A\}\text{,}\) where \(w_a,w_{\varphi(a)}\) are choices of words in \(X^{\pm 1}\) representing the elments \(a,\varphi(a)\) in \(G\text{,}\) induce by Lemma Lemma 1.6.1 a natural homomorphism \(\psi:G \to G*_t\text{.}\) We need to show that \(\psi\) is injective.

Suppose towards a contradiction that \(\psi\) was not injective. Then there is some \(g \in G\setminus\{1\}\text{,}\) of minimal word length, such that \(\varphi(g)\neq 1\text{.}\) By van Kampen's Lemma (Theorem 3.1.7) there is some reduced word \(w_g\) (realizing minimal word length) which is the boundary word of a van Kampen diagram \(\mathcal D\) whose 2-cells have boundary words from \(R \into R \cup\{t^{-1}w_at(w_{\varphi(a)})^{-1}\mid a \in A\}\text{.}\)

Because \(g \neq_G 1\text{,}\) \(\mathcal D\) cannot consist solely of 2-cells with boundaries from \(R\text{,}\) therefore \(\mathcal D\) must contain HNN-2-cells and therefore at least one dual \(t\)-tracks. Let \(\mathcal D\) such a diagram with a minimal number of tracks. Because the boundary word of \(\mathcal D\) is a word containing letters only in \(X\) none of the tracks can reach the boundary of \(\mathcal D\text{,}\) so they must all be cicrcles.

Let \(\tau \subset \mathcal D\) be an innermost circular track, i.e. it doesn't enclose any other circular tracks. The union of 2-cells containg it for an annulus \(\mathcal A\) with an inner boundary word \(w^{in}\) and an outer boundary word \(w^{out}\text{.}\) Now note on the one hand that, without loss of generality, \(w^{in}\) is a product of elements in \(A\) therefore \(w^{in} \in A\) and \(w^{out} = \varphi(w^{in})\text{.}\) On the other hand \(w^{in}\) is the boundary word of a van Kampen (sub) diagram, and since \(\tau\) is innermost there are no HNN-2-cells, so all 2-cells in the subdiagram have boundary labels in \(R\text{.}\) This means that \(w^{in} =_G 1\) and since \(\varphi A \to A'\) is an isomorphism we have that \(w^{out}=_G 1\) as well. Therefore by van Kampen's lemma we can find a van Kampen diagram \(\mathcal{D}'\)with 2-cells with boundary in \(R\) whose boundary word is \(w^{out}\text{.}\)

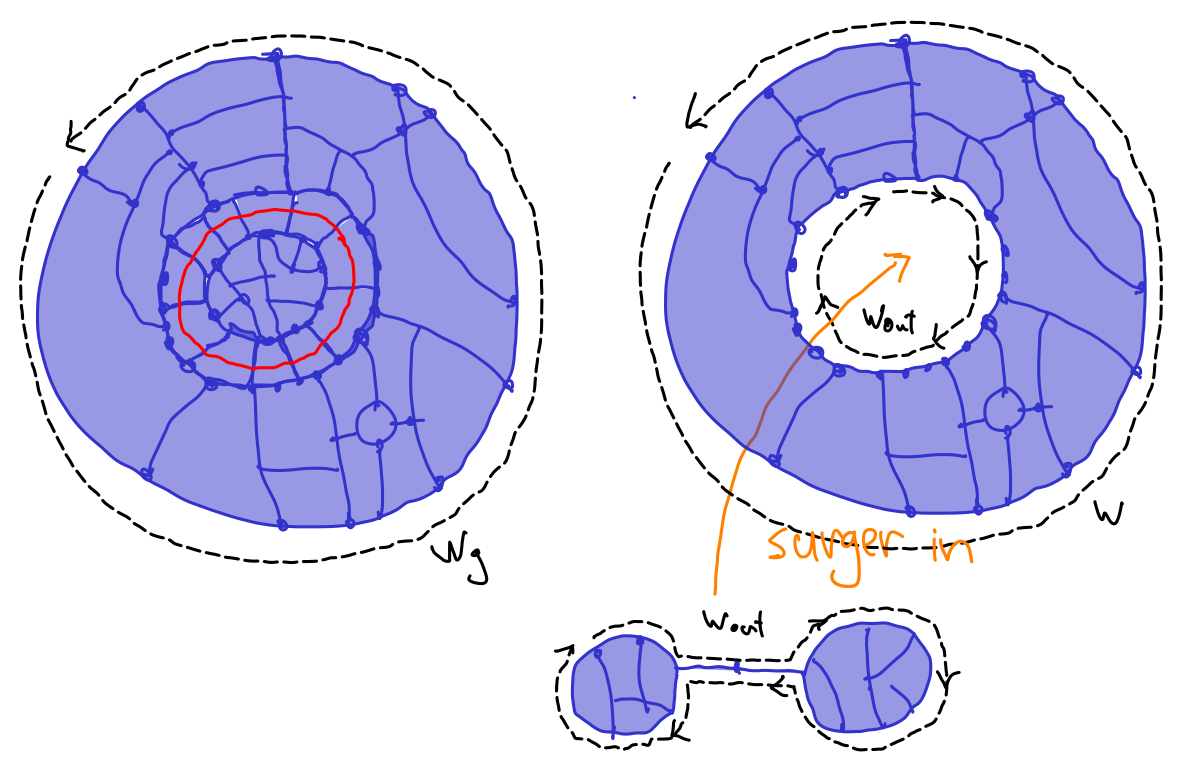
It follows that we can cut out the annulus \(\mathcal A\) and surgically re-attach \(\mathcal D'\text{.}\) The resulting van Kampen diagram is a witness of the triviality of \(w_g\) in

\begin{equation*} G*_t=\pres{X,t}{R,t^{-1}at = \varphi(a); a\in A }, \end{equation*}

with one less track than \(\mathcal D\text{,}\) but this contradicts the fact that \(\mathcal D\) had a minimal number of tracks.

In fact, the main thrust of the proof of the previous Theorem can be restated as the following lemma:

Next we have this other injectivity result for the mapping \(\ZZ \to \gen t\text{:}\)

Suppsose towards a contradiction that \(t^n=1\) form some \(n>0\text{.}\) Then \(t^n\) is the boundary word of a van Kampen diagram \(\mathcal D\text{.}\) This means that there are tracks starting and ending on the boundary of \(\mathcal D\text{,}\) but since the 2-cells containing containing tracks are HNN-2-cells, Figure 3.2.10 below shows that any such track \(\tau\) must lie in a "twisted strip".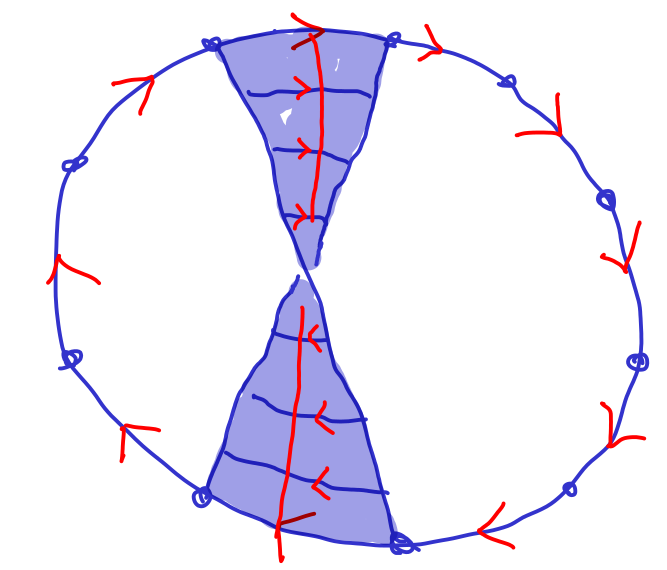

This contradicts the planarity of \(\mathcal D\text{,}\) or the fact that \(\tau\) cuts \(\mathcal D\) into two components.

Subsection 3.2.3 Economical presentations and (some of) the secrets of \(\mathrm{BS}(1,2)\)

The presentation (3.2.1) for \(G*_t\) may have infinitely many relators, one for each element in \(A\text{.}\) Until now, this infinite presentation has been convenient, but seeing as we are primarily interested in finitely presented groups, it will be nice to get a criterion for when an HNN extension is also finitely presented.

So now let's turn our attention to the following little presentation:

Let's show that it is an HNN extension.

We first note that \(\ZZ \approx \pres{a}{}\text{.}\) Now \(\pres{a}{}\) contains the subgroups \(\gen a\text{,}\) i.e. the whole thing, and \(\gen{a^2}\text{,}\) i.e. \(2\ZZ\text{.}\) Both of these subgroups are isomorphic to \(\ZZ\) and we can take the isomorphism:

Recall that a homomorphism is fully determined by the image of a generating set.

Therefore \(\mathrm{BS}(1,2)\) is an HNN extension of the cyclic group. In particular we have an injective homomorphisms

so \(a\) has infinite order in \(\mathrm{BS}(1,2)\text{.}\) This fact was what was missing in Example 2.2.7. Now we have proved the existence of a group that is "algebraically" embedded into another group, but such that the inclusion is not a quasi isometric embedding.

Actually, the simplest examples of distorted subrgroups (i.e. subgroups that are not quasi isometrically embedded) arise from HNN extensions.

Similarly, we see that the other Baumslag-Solitar groups

are also infinite and the element \(a\) has infinite order. Note that here although we used the letter \(b\) instead of \(t\text{,}\) we still have the HNN extensions structure.

Subsection 3.2.4 Syllables and Britton's lemma.

Our treatment of HNN extensions, using van Kampen diagrams and tracks, is not historical. In this final section we will give some classical notation and the main classical result regarding HNN extensions.

Suppose that we are given \(G = \pres X R\) then every element in \(G*_t\) can be represented as a word of the form

where the subwords \(a_i\) are words in \(X^{\pm 1}\text{,}\) \(t\) is the stable letter, and the \(n_i \in \ZZ\text{.}\) The words \(a_i\) are called \(G\)-syllables.

If we are more explicit and identify \(A,A' \leq G\) and \(\varphi:A \to A'\) so that \(\varphi(a) = t^{-1}at; a \in A\) then we say that a word \(w\) can be pinched if it contains a subword

where \(a_i \in A'\) or \(a_j \in A\text{.}\) In this case we can reduce the numner of occurrences of \(t\) via

For this reason we will say that a word in an HNN extension is reduced if it doesn't contain any pinches. We now finish by stating what is the classical fundamental theorem of HNN extensions:

In particular reduced words in HNN extensions are non-trivial. At this point there is enough machinery so that an interested reader could consult Chapter 9 of [6] to see how to contruct a group with undecidable word problem.