Skip to main content

Section 3.1 van Kampen diagrams and the geometry of the word problem

Let us now turn our attention back to finitely generated groups given by relations:

\begin{equation*} G = \pres X R. \end{equation*}

In Section 1.4 we say that any word representing the identity in \(G\) was equal in \(F(X)\) to a product of conjugates of elements of \(R^{\pm1}\text{.}\) In Section 1.8 in we saw that every element in \(F(X)\) was conjugate to a cyclically reduced element and that all cyclic permutations of an element are conjugate. With this in mind we have the following two-dimensional notion: an \(X\)-directed 2-cell, or just briefly a 2-cell, is a cyclic \(X\)-digraph enclosing a topological disc.

Figure 3.1.1. A 2-cell

As defined, we note that a 2-cell has no preferred orientation or vertex. Thus, for a given boundary word \(r\text{,}\) the same 2-cell represents every cyclic conjugate of \(r^{\pm 1}\text{.}\) A diagram is 2-complex, i.e. a graph to which is attached 2-cells. A planar embedding of a diagram is a specific way of embedding/drawing a diagram in the plane. We will often abuse notation say planar diagram instead of "diagram equipped with a planar embedding". We will say that a planar diagram is simply connected if, informally, it has no holes, or if every cycle in the underlying graph is filled with discs. Noting that a diagram is a CW 2-complex, "simply connected" is perfectly well-defined.

We point out that most of graphs shown in the previous section are definitely not simply connected.

Figure 3.1.2. Some planar diagrams. Can you pick out the simply connected one? Note that we will sometimes omit drawing directions and labels of edges.

Subsection 3.1.1 van Kampen diagrams

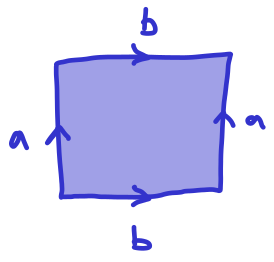
A van Kampen diagram is a simply connected planar diagram. The planar embedding gives rise to a boundary word, which is the label of the path that can be read clockwise around the boundary. We note that the boundary word is well up to cyclic permutation.

Figure 3.1.3. The boundary word is the label of the path read clockwise around the boundary.

Van Kampen diagrams are the most important tool in studying the word problem in groups. First note that if some word \(w\) represents the identity in \(\pres X R\text{,}\) then

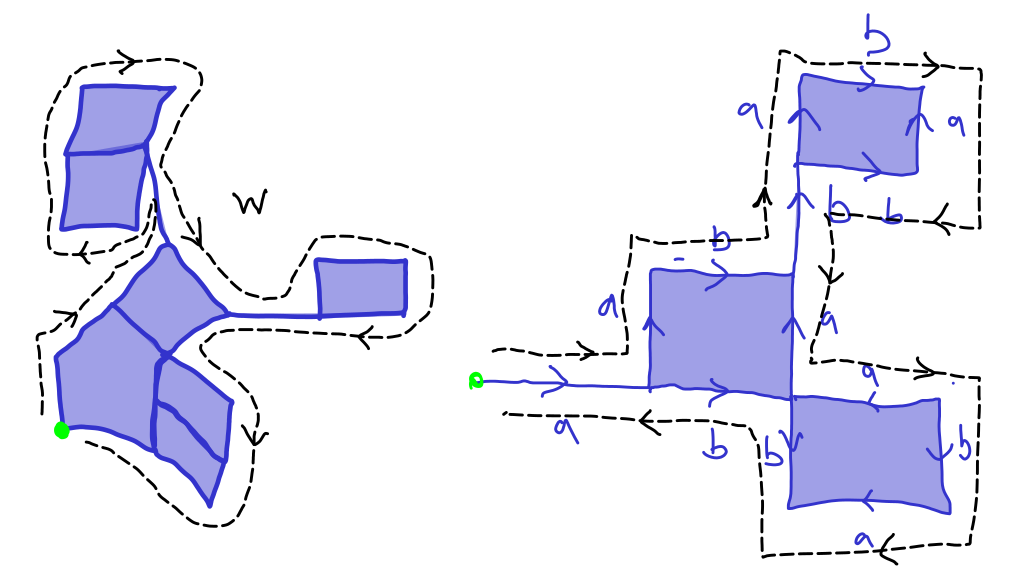
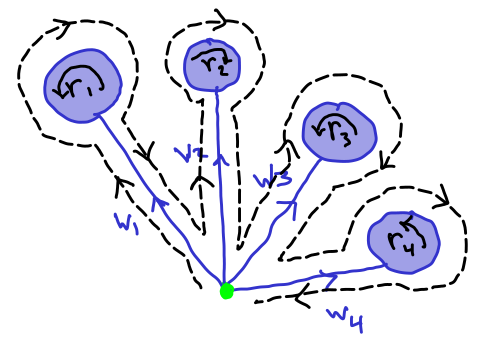
\begin{equation*} w =_{F(X)} \prod_{i=1}^{k}w_ir_i^{\epsilon_i} w_i^{-1} \end{equation*}

for some conjugates of \(r_i^{\pm 1}\in R\text{.}\) We can therefore form a balloon diagram as in Figure 3.1.4 whose boundary word is precisely the (unreduced product) \(\prod_{i=1}^{k}w_ir_i^{\epsilon_i} w_i^{-1}\text{.}\)

Figure 3.1.4. A balloon diagram whose boundary word \(w_1 r_1^{-1} w_1^{-1} w_2 r_2 w_2^{-1} w_3 r_3^{-1}w_3^{-1} w_4 r_4^{-1} w_4^{-1}.\)

Let \(\mathcal D\) be a van Kampen diagram whose 2 cells are bounded by words \(r \in R.\) Then the boundary word \(w\) of \(\mathcal D\) represents the trivial element in \(\pres X R\text{.}\) See Figure 3.1.5, for example.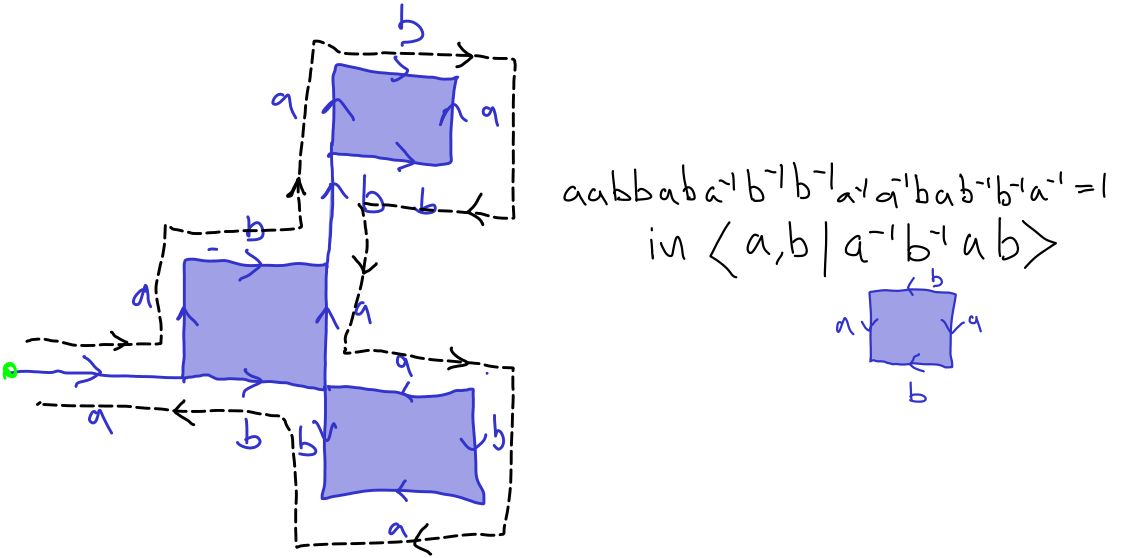

Figure 3.1.5. A balloon diagram whose boundary word \(w_1 r_1^{-1} w_1^{-1} w_2 r_2 w_2^{-1} w_3 r_3^{-1}w_3^{-1} w_4 r_4^{-1} w_4^{-1}.\)

The reason is that any such diagram can be "unfolded" to a balloon diagram (see Figure 3.1.6). This witnesses that a boudary word \(w\) is equal to a product

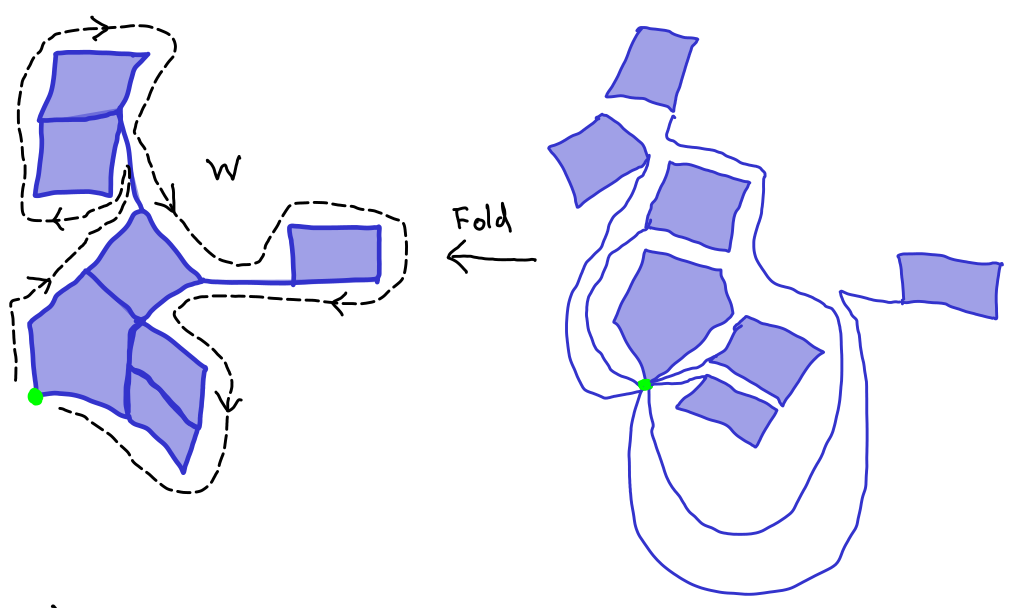
Figure 3.1.6. Unfolding a van Kampen diagram to a balloon diagram.

This unfolding fact and its converse give van Kampen's Lemma. The main difficulty resides in the fact that when folding a balloon diagram, some 2-cells can get folded "all the away around" creating spheres (think of a soccer ball.) The argument is to show that if we start with a balloon diagram with a minimal number of 2-cells, by performing the foldings corresponding to elementary reductions in boundary words, we remain planar at every step. Otherwise we could have removed 2-cells.

Exercises 3.1.2 Exercises

1.

Let \(X\) be some alphabet and let \(T\) be an \(X\)-digraph which is a tree. Prove that the boundary label is a word that is equal in \(F(X)\) to the identity.

Hint: A spur is a vertex with degree 1. Perform elementary cancellations one at a time. Show at each step that the word obtained from an elementary cancellation can be obtained by deleting a spur and incident edge in a tree and taking the new boundary word.

2.

"Unfold the van Kampen diagram in Figure 3.1.5 an explicitly express that word as a product of 3 conjugates of \((a^{-1}b^{-1}ab)^{\pm 1}\)

3.
Show that if two word \(w,w'\) are reduced words that are equal in \(\pres X R\) then there is a "possibly pinched bigon" along whose top we can read \(w\) and along whose bottom we can read \(w'\) that can be filled with 2-cells bounded by words in \(R\text{.}\)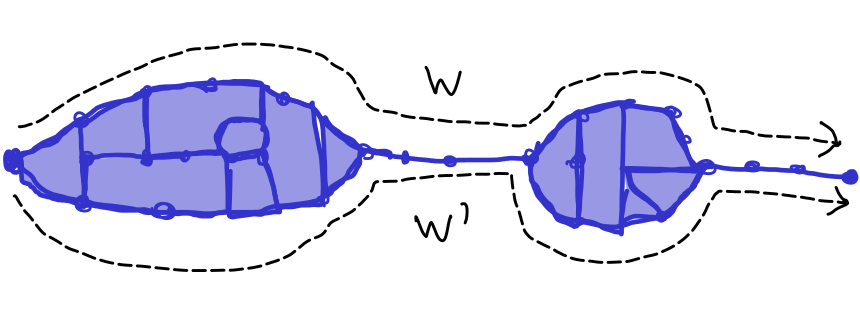
Figure 3.1.8. A possibly pinched bigon
4.

In Section 1.6 you were asked to show that in \(\pres{r,\rho}{\rho\rho\rho,rr,r\rho r\rho}\) we have \(r\rho = \rho^2 r\text{.}\) Construct the bigon witnessing this fact.