Section 1.5 Cayley graphs
So far we have been very combinatorial. Let's get geometric! First recall that a directed graph \(Z\) consists of a set \(V\) of vertices and a set \(E \subset V\times V\) of directed edges. If we want we can also label the directed edges using some symbol from some alphabet.
Given a generating set \(S\subset G\) of a group \(G\) we can form a Cayley graph, denoted \(\cay S G\text{,}\) by taking the vertex set be the set \(G\) itself and for each \(a \in S\) and each \(g \in G\) we draw the directed edge labelled \(a\) from \(g\) to \(ga\text{:}\)
Let's do an example. Consider \(D_{2\times 3}\text{,}\) the dihedral group of order 6, or the symmetry group of the triangle. It is generated by \(\rho\text{,}\) the clockwise rotation by \(120^\circ\text{,}\) and \(r\) the reflection about the vertical axis. We let \(D_{2 \times 3}\) act on the left.
It is known that \(D_{2\times 3}\) has 6 elements, we draw its Cayley graph \(\cay{\{\rho,r\}}{D_{2\times 3}}\) here where next to each vertex \(g \in G\) we have the result of applying \(g\) to the triangle. 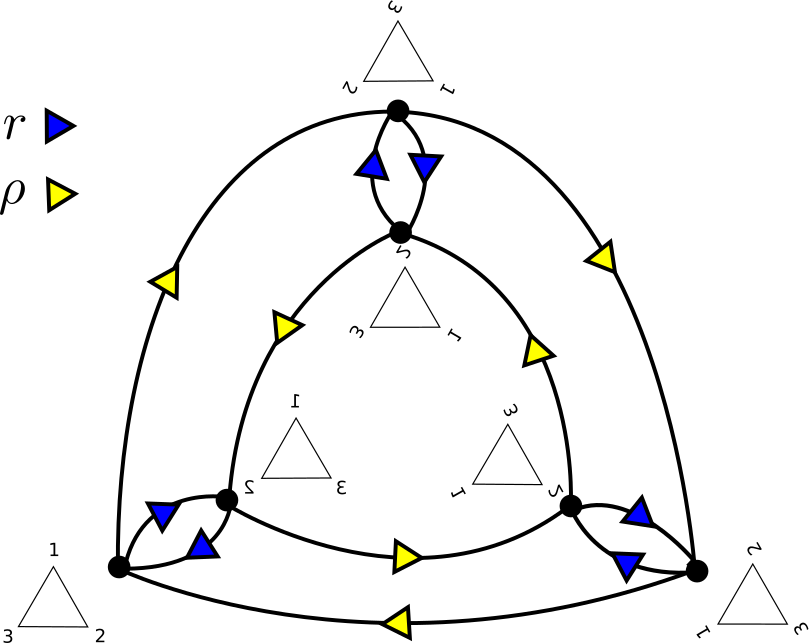
Because they are highly symmetric, Cayley graphs are aesthetically pleasing, and they essentially play the role of a multiplication table in a group. Unfortunately (see Exercise 1.5.1.1) a group has multiple Cayley graphs, depending on the choice of generating set.
Infinite groups also have Cayley graphs. Consider for example \(\ZZ\oplus\ZZ = \ZZ^2\) which is the set
equipped with component-wise addition. If we take generators \(a =
(1,0)\) and \(b=(0,1)\) then \(\cay{\{a,b\}}{\ZZ^2}\) looks like: 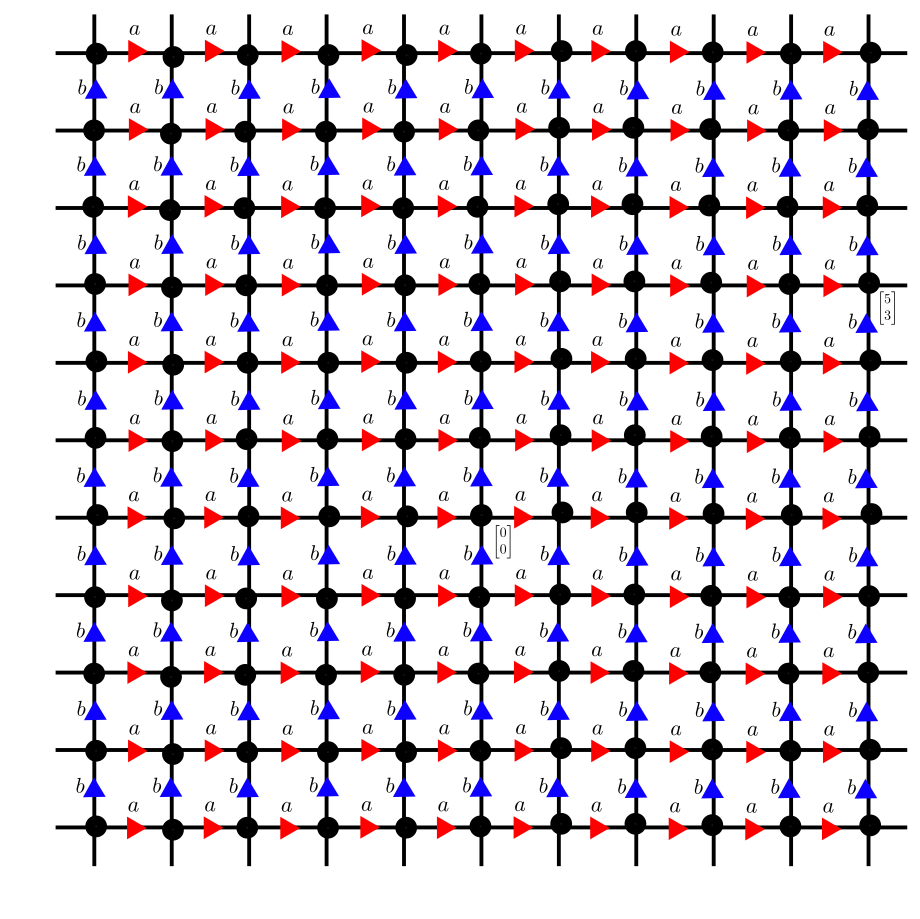
Every edge \(e\) in a directed labelled graph has an initial vertex \(\iota(e)\text{,}\) a terminal vertex \(\tau(e)\) and a label \(\lab(e)\text{.}\) For example if \(e=(u,v)\text{,}\) where \(u,v\) are vertices then \(\iota(e)=u,\tau(e)=v\text{.}\) We may define the formal inverse \(e^{-1}\) of an edge \(e\) so that \(\tau(e)=\iota(e^{-1})\) and \(\tau(e^{-1})=\iota(e)\) and the label \(\lab(e^{-1}) = \lab(e)^{-1}.y\)
A path in a directed graph \(Z\) with edge set \(E\) is a sequences of edges and formal inverses:
that "connect together", i.e. \(\tau(e_i) = \iota(e_{i+1})\) for \(1\leq i \lt n\text{.}\) The initial point of a path is the vertex \(\iota(e_1)\) and the terminal vertex is the vertex \(\tau(e_n)\text{.}\) We say that the path \(\alpha\) goes from its initial vertex to its terminal vertex. Here's an example:
A path is said to be reduced if it has no subpaths of the form \(e e^{-1}\) for some \(e \in E^{\pm 1}\text{.}\)This is similar to our treatment of words in an alphabet. The only distinction is that you can only concatenate paths if one starts where the other ends. Otherwise there is associativity and even a reduction procedure where we successively delete subpaths of the form \(ee^-1\) which we can call tightening. Everything works out like in Section 1.2, we can even define inverses. Such a structure, which is almost like a group except that multiplication is not always defined is called a groupoid.
If the reader has any experience with fundamental groups in topology, then this should also look familiar, as all we are doing here is giving a combinatorial treatment of a path:
where the graph \(Z\) is thought of as a topological space. Specifically, a CW complex with 0 and 1 dimensional cells.
Given a path \(\alpha = e_1\cdots e_n\text{,}\) we will say that its length is \(n\text{,}\) the number of edges is contains and its label is the word
The whole point of Section 1.2 was that in a free group on a specified alphabet distinct reduced words correspond to distinct elements. Once relations are added this is no longer the case. Indeed if \(G = \pres X R\) and given two distinct reduced words \(w\) and \(w'\) in the alphabet \(X\) it may be that \(w \neq_{F(X)} w'\) (i.e. they are distinct reduced words) but that viewed as products of generators of \(G\) we have \(w =_G w'\text{,}\) i.e. they have the same image via the standard map \(F(X) \to \pres X R\text{.}\)
The Cayley graph illustrates this nicely:
Lemma 1.5.3.
Let \(S \subset G\) be generating set. Let \(\beta\) be a path in \(\cay S G\)that goes from the identity \(1\) to some element \(g \in G\) (recall that the vertices of \(\cay S G\) are the elements of \(G\)) then, viewed as a product of element in \(S^{\pm 1}\) we have:
Proof.
Let \(\beta:e_1\cdots e_n\) and let \(\lab(e_i) = a_i \in S^{\pm 1}\text{.}\) Then by the definition of a Cayley graph we have
Exercises 1.5.1 Exercises
1.
It is well-known that \(D_{2\times 3} \approx S_3\text{,}\) the group of permutations of the set \(\{1,2,3\}\text{.}\) \(S_3\text{,}\) like any symmetric group, is generated by permutations. Using cycle notation we have
Draw the Cayley graph \(\cay{\{(1,2),(2,3)\}}{S_3}\) and compare it with the Cayley graph for \(D_{2\times 3}\) shown above.
2.
We always have \(\gen G = G\text{.}\) What does \(\cay G G\) look like?
3.
Let \(S\subset G\) be a generating set. Let \(d:G\times G \to \RR\) be the function defined as \(d(g,h)=m\text{,}\) where \(m\) is the length of the shortest path in \(\cay S G\) from \(g\) to \(h\text{.}\)
Show that \(d\) is a metric on \(G\text{.}\) This metric is called the word metric on \(G\text{.}\)
4.
The group \((\ZZ,+)\) is generated by \(1\) (here the identity is 0, so that \(1_\ZZ = 0\)). Consider the generating set \(\{1,10\} = \{a,b\}\) of \(\ZZ\text{.}\)
Sketch \(\cay{\{a,b\}}\ZZ\text{.}\) What can you say about the ball of radius 4 about the identity in \(\cay{\{a,b\}}\ZZ\) compared to the ball of radius 4 about the identity in \(\cay{\{a,b\}}{\ZZ^2}\)
5.
Let \(X\) be a finite alphabet, let \(F(X)\) be the free group on \(X\) and consider \(X\) as a generating set of \(F(X)\text{.}\) Prove that \(\cay{X}{F(X)}\) is a tree.
Hint: A tree is a connected graph without any cycles. The label of a cycle in a group's Cayley graph must be reduced product that equals the identity.
