Skip to main content

Section 2.5 Appendix: Some final facts about quasi-isometry

Although we will now move on to other topics, there are a few facts the author cannot continue to ignore.

Subsection 2.5.1 Counting ends, easy as \(0, 1, 2, 2^{\aleph_0}\)

Although it's easy to come up with graphs that any number of ends, take for example an infinite tripod, for groups the situation is more restrictive. Suppose that \(G\) has more than two ends, then for some Cayley graph \(X = \cay A G\) there is some finite ball \(B = B(1,r_0)\) about the identity such that \(X \setminus B\) has at least three infinite components:

Figure 2.5.1. A finite essential disconnecting ball in a Cayley graph with more than two infinite complementary components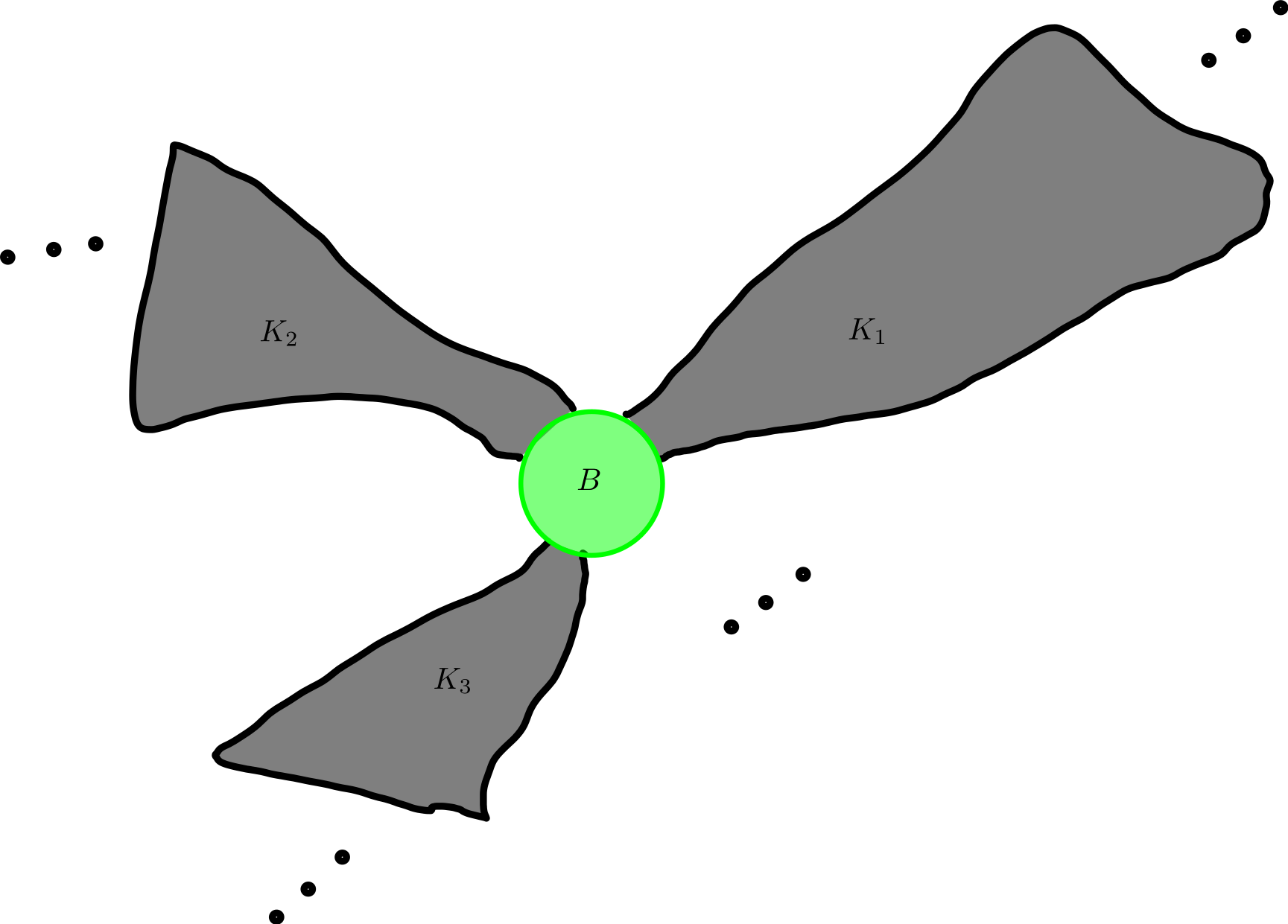

Because a finitely generated group always acts freely (and therefore properly) on its own Cayley graphs we find that we can always find elements that will "push" \(B\) off itself and we have the following tree-like structure: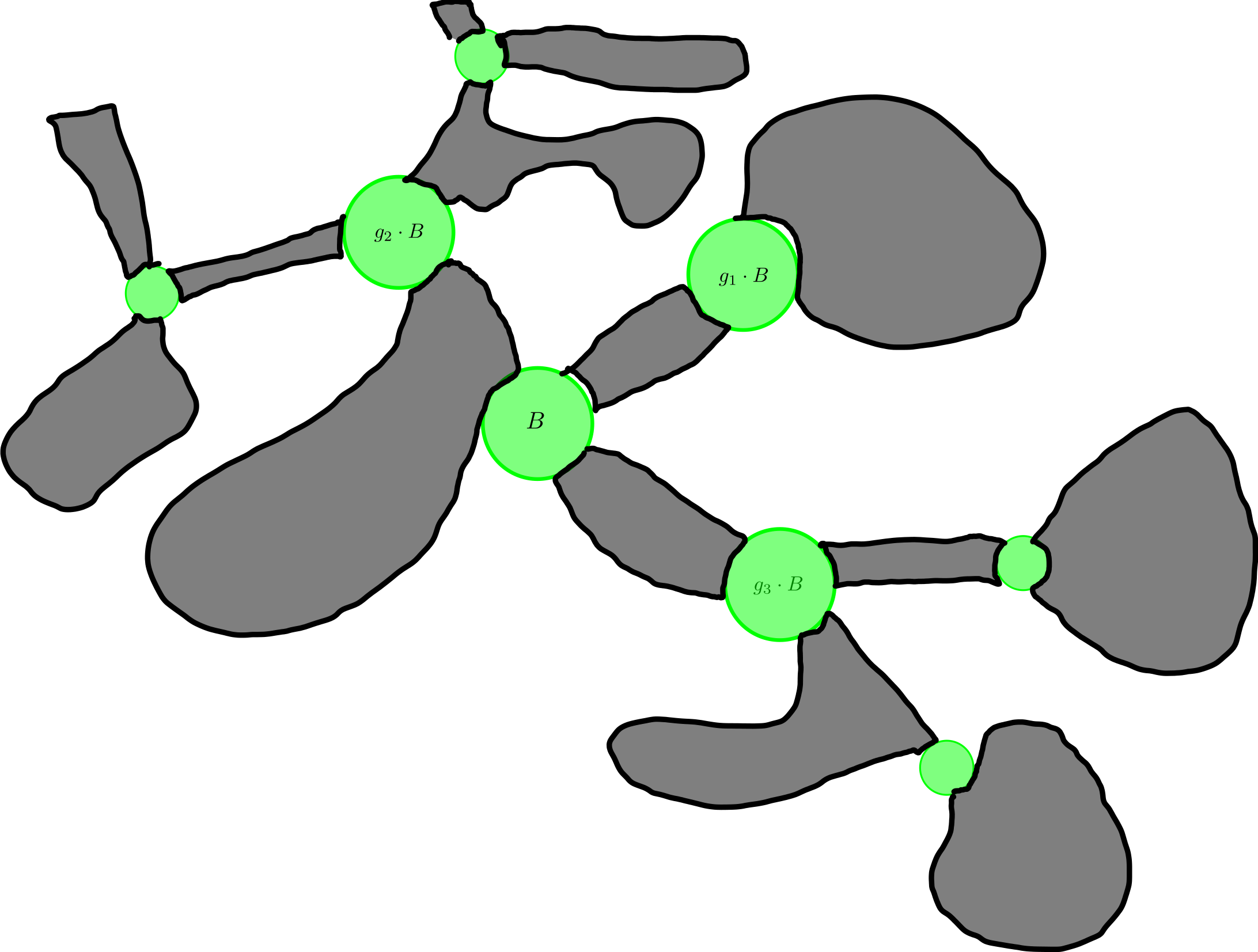

Figure 2.5.2. Disjoint translates of an essential disconnecting ball.

Given this picture, it is immediate that as we take compact exhaustions of \(X\) the number of infinite components of complements goes to infinity, therefore if \(|\mathrm{Ends}(G)|>2\text{,}\) then \(|\mathrm{Ends}(G)|=\infty,\) and it is easy to see that this infinite cardinality must be continuum or \(2^{\aleph_0}.\)

Subsection 2.5.2 The topology of \(\mathrm{Ends}(G)\)

As we saw, ends correspond to an infinite chains \(K_1\supset K_2 \supset \cdots\) of infinite components. Since these are complements of exhaustions we must have for a given end

\begin{equation*} \bigcap_{i=1}^\infty K_i = \emptyset. \end{equation*}

The inverse limit construction, is what lets us get "something from nothing". Nonetheless, given some compact essential disconnecting set \(C \subset X\) it makes sense to think of an end as lying in some component of \(X\setminus C\text{,}\) formally we can think of some decreasing sequence of infinte components eventually lying in some component of \(X \setminus C\text{.}\) This lets us put a topology on \(\mathrm{Ends}(X)\text{,}\) for some graph. Let \(C \subset X\) be a compact set and let \(K \subset X\setminus C\) be an infinite component. Then we have an open set \(U_C \subset \mathrm{Ends}(X)\) consisting of all ends that "lie" in \(C\text{.}\) The topology can be informally, yet accurately, described as follows: two ends are "close" only if they are separated by a "large" ball about the identity.

Here are interesting facts:

  • A quasi isometry \(f: X\to Y\) induces not only a bijection, but in fact, homeomorphism \(\hat f:\mathrm{Ends}(X) \to \mathrm{Ends}(Y)\)
  • In the case where \(X = \cay A G\text{,}\) then the topology on \(\mathrm{Ends}(X)\) is that of a Cantor set.
  • When \(X\) is an infinite tree \(X \cup \mathrm{Ends}(X)\) can be topologized as a compactification of \(X\text{,}\) which is natural in the context of metric spaces. An example we say is compactifying \(\RR\) with the points \(\pm \infty\text{.}\)
  • Certain groups admit refinements of ends which are also quasi isometric invariants, known as boundaries, which enable many stronger quasi isometric rigidity results.

Subsection 2.5.3 Gromov's polynomial growth theorem

Let us denote the commutator \([x,y] = x^{-1}y^{-1}x,y\text{,}\) and the \(n\)-fold commutator

\begin{equation*} [x_1,x_2,\cdots,x_m] = [x_1,[x_2,\cdots,x_n]]\text{.} \end{equation*}

A group \(N\) is said to be nilpotent of class \(c\) if every \((c+1)\)-fold commutator is trivial. For example abelian groups are precisely nilpotent of class 1.

The reader may have seen the class of solvable groups before and it would be natural to think that solvable and nilpotent are the same thing, but they're not. Nilpotent implies solvable, but not the other way around.

Previously we saw that for the abelian groups \(\ZZ^n\text{,}\) the amount group elements contained in a ball \(B(1,r)\) with respect to some word metric grew like a polynomial. Since quasi isometries distort distances linearly and that the composition \(f\circ l\) of a degree \(d\) polynomial \(f\) and a linear function \(\ell\) is still a degree \(d\) polynomial, it can be shown that the degree of polynomial growth of balls is a quasi isometric invariant of groups. This phenomenon is called polynomial growth.

Not all groups have polynomial growth, for example, the number of elements a ball of radius \(r\) in \(F(a,b)\) grow exponentially.

So far we have focused on quasi isometry as applied to a single group, and asked to which extent does a quasi isometry class determine the algebraic properties of the group. There are many other results about classes of groups such as the following.

We first note that due to the fundamental limitations of quasi isometry, it is impossible to make such a statement without the "virtually" qualification. Secondly, we note that this is a very strong algebraic conclusion based solely geometry. Finally, the way this is proved uses very cool machinery that is unlike anything that will be covered in this course.