Skip to main content

Section 3.5 The \(C'(1/6)\) small cancellation condition and Dehn's algoithm

Let us now put combinatorial curvature to work. Let \(G = \pres X R\) and suppose \(X,R\) are finite, that all words in \(R\) are cyclically reduced and furthermore that no \(r \in R\) is a consequence of the remaining relations. A piece is a subword of some \(r \in R\) which either occurs in some other \(r' \in R\) or which occurs in a different location in \(r\text{.}\)

Another way of considering pieces is to consider a van Kampen diagram \(\mathcal D\) without cancellable pairs (see Figure 3.5.1).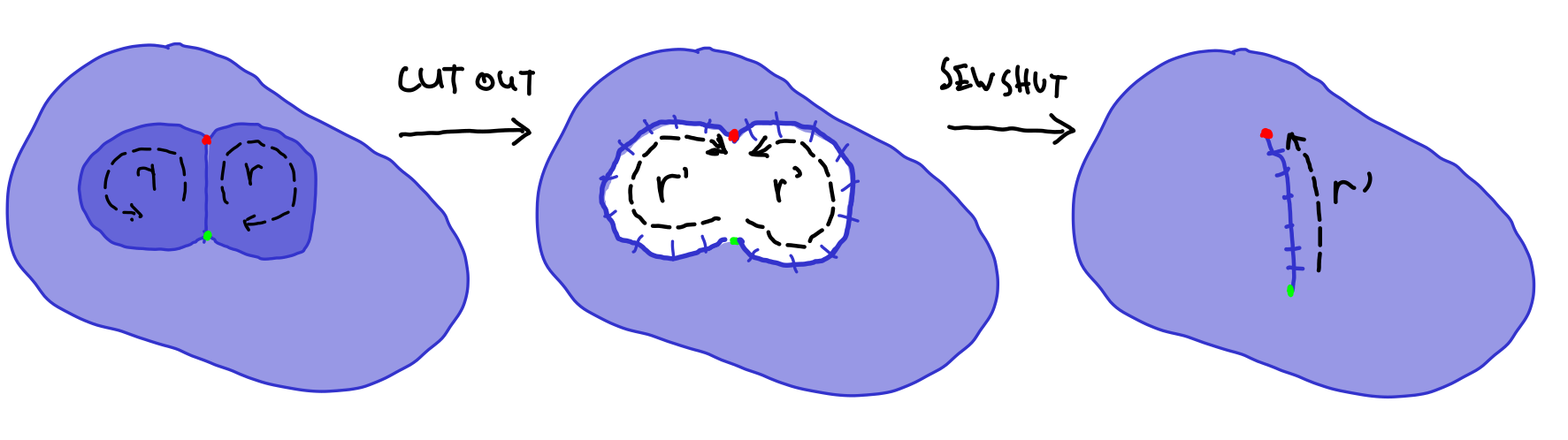

Figure 3.5.1. A cancellable pair in a van Kampen diagram and how to remove it.
A arc is a maximal connected subgraph whose vertices have degree at most 2, an internal edge is an edge contained in the boundaries of two 2-cells, and an internal arc is an arc consisting of internal edges. Then pieces are exactly the labels internal arcs of van Kampen diagrams over \(\pres X R\text{.}\)

Obviously there are many pieces, any symbol that occurs twice in \(R\) is a piece. The small cancellation condition has to do with proportionately large pieces.

Definition 3.5.2.

A presentation \(\pres X R\) satisfies the \(C'(\lambda)\) metric small cancelation condition if for any \(r \in R\) and any piece \(p\) which is subword of \(r\) we have

\begin{equation*} \frac{|p|}{|r|} \lt \lambda, \end{equation*}

where \(|p|,|r|\) denote word lengths.

Now this condition interests us because whenever it is satisfied by a presentation, we will have a uniform method to solve the word problem. Before going into details let's explain the what will happen.

The word problem on \(\pres X R\) is difficult to solve when there are words representing the trivial which are relatively short but whose van Kampen diagrams contain many, many 2-cells. We can think of this as a small perimeter enclosing a large area. For example one could justifiably draw a circle on the ground around oneself and declare that this circle encloses the rest of the surface of the earth.

In a space, the relationship between areas enclosed by some perimeter is given by something called an isoperimetric function. For example in the Euclidean plane \(\mathbb{E}^2\) given closed loop of length \(\ell\text{,}\) the maximal area that can be enclosed is \(A=\frac{1}{4\pi}\ell^2\text{.}\) So we'll say that \(\mathbb{E}^2\) has a quadratic isoperimetric function.

Now as we saw, on a sphere (which is positively curved) we have regions whose areas are much larger than the length of bounding curve. On the plane (which has zero curvature) area is at most quadratic in the length of a bounding curve. In the presence of negative curvature, area is a linear function of the length of a bounding curve.

As far as group theory is concerned, these concepts appear in van Kampen diagrams. We consider the length of the boundary word of a van Kampen diagram to be the length of an enclosing curve and we consider the area to be the number of 2-cells. In this case negative curvature manifests itself as follows: a reduced word \(w\) representing the identity in \(\pres X R\)can be written as the product of at most \(C\cdot|w|\) conjugates of relations. We will now present something which is a special case of a result known as Greendlinger's Lemma.

Subsection 3.5.1 Finding and removing shells

For this section we'll assume that \(\pres X R\) be a \(C'(1/6)\) presentation. Before considering we shall make the following modification to van Kampen diagrams: we will merge all the arcs appearing in a diagram to a single edge, the label of the resulting edge will be the word read along the arc. We will call such a diagram arc reduced. We note that there are no longer any vertices of degree 2 in an arc reduced diagram. For the moment we will also restrict our attention to van Kampen diagrams that are homeomorphic to discs, i.e. which cannot be disconnected by removing a vertex.

Let \(\mathcal D\) be an arc reduced van Kampen diagram homeomerphic to a disc. We will say that a vertex \(v\) is interior if is in the interior of \(\mathcal D\text{,}\) otherwise we say that \(v\) is exterior. Given a 2-cell \(f\) we will say that \(f\) is internal if all the (open) edges in its boundar contained in the interior of \(\mathcal D\text{,}\) otherwise we say it is external. We note that for an internal 2-cell \(f\text{,}\) all the arcs in its boundary consist of pieces. By the \(C'(1/6)\) condition, all these arcs have length strictly less than \(1/6\) the length of the boundary word of the 2 cell, therefore internal 2-cells must have at least 7 sides. We now come to a more technical definition:

Definition 3.5.3.
Let \(\mathcal D\) be an arc-reduced van Kampen diagram homeomorphic to a disc. We say that a 2-cell \(f\) is an \(i\)-shell if its boundary only contains one external arc, and if it is joined to the rest of the diagram by a path consisting of \(i\)arcs.

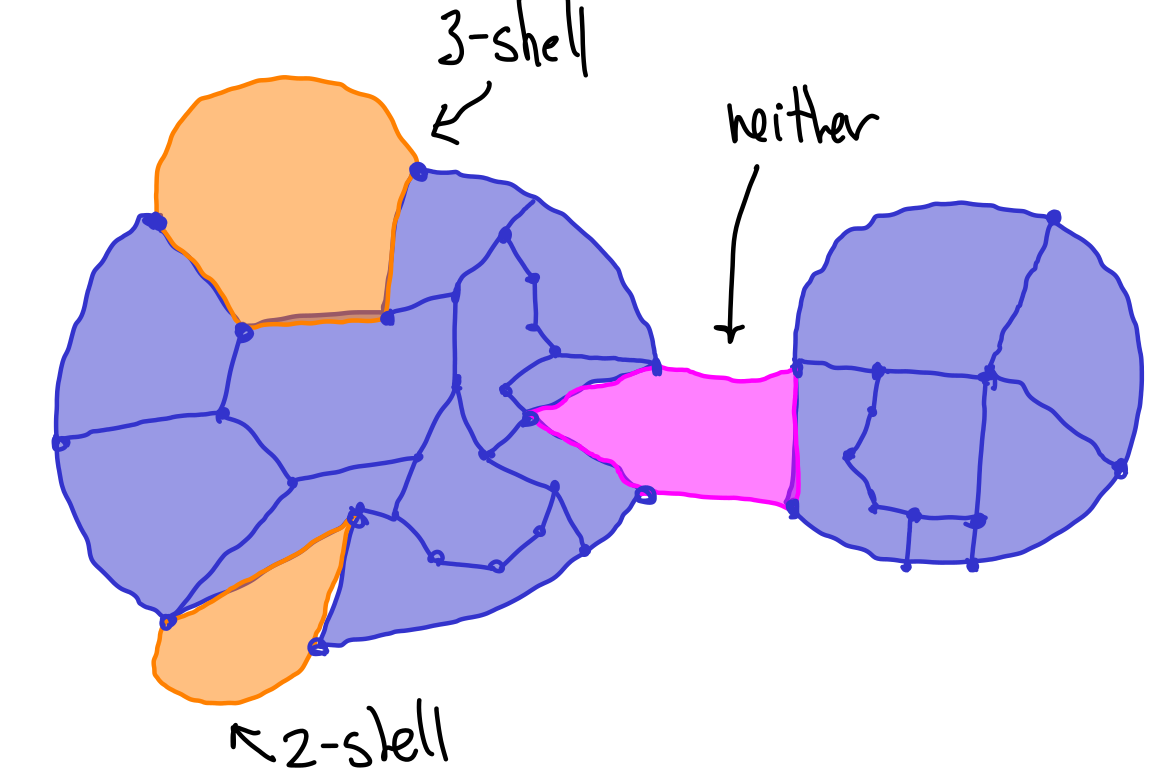
Figure 3.5.4. Some \(i\)-shells and an external 2-cell isn't an i-shell.

Now, recalling that labels of arcs pieces and that pieces are less that 1/6 the length of any relator they are part of, for an \(i\leq 3\) shell we see that the length of the union of internal arcs attaching it to the rest of the diagram is less than the length of the external arc (\(3\times (\lt 1/6) \lt 1/2\)) so the effect of removing an \(i\)-shell so to produce a new van Kampen diagram with fewer 2-cells and a strictly shorter boundary word.

Our goal is now to show that the \(C'(1/6)\) small cancellation condition always forces arc-reduced van Kampen diagrams homeomorphic to circles to have \(i\)-shells for some \(1 \leq i \leq 3\text{.}\) We will find these using curvature.

In the previous lecture we saw that \(\chi(\mathcal D) = 1\text{,}\) therefore \(\mathrm{Curvature}(\mathcal D) = 2\pi>0\text{.}\) For reference consider the following regular Euclidean polygons:

  1. Triangle, angle sum \(\pi\text{,}\) average angle \(\pi/3\text{.}\)
  2. Square, angle sum \(2\pi\text{,}\) average angle \(\pi/2\)
  3. Pentagon, angle sum \(3\pi\text{,}\) average angle \(3\pi/5\)
  4. Hexagon, angle sum \(4\pi\text{,}\) average angle \(2\pi/3\)
  5. Heptagon, angle sum \(5 \pi\text{,}\) average angle \(5\pi/7\)

In our context, recall that for a 2-cell we have that \(\mathrm{Curvature}(f)\) is the angle sum in excess of the expected Euclidean angle sum.

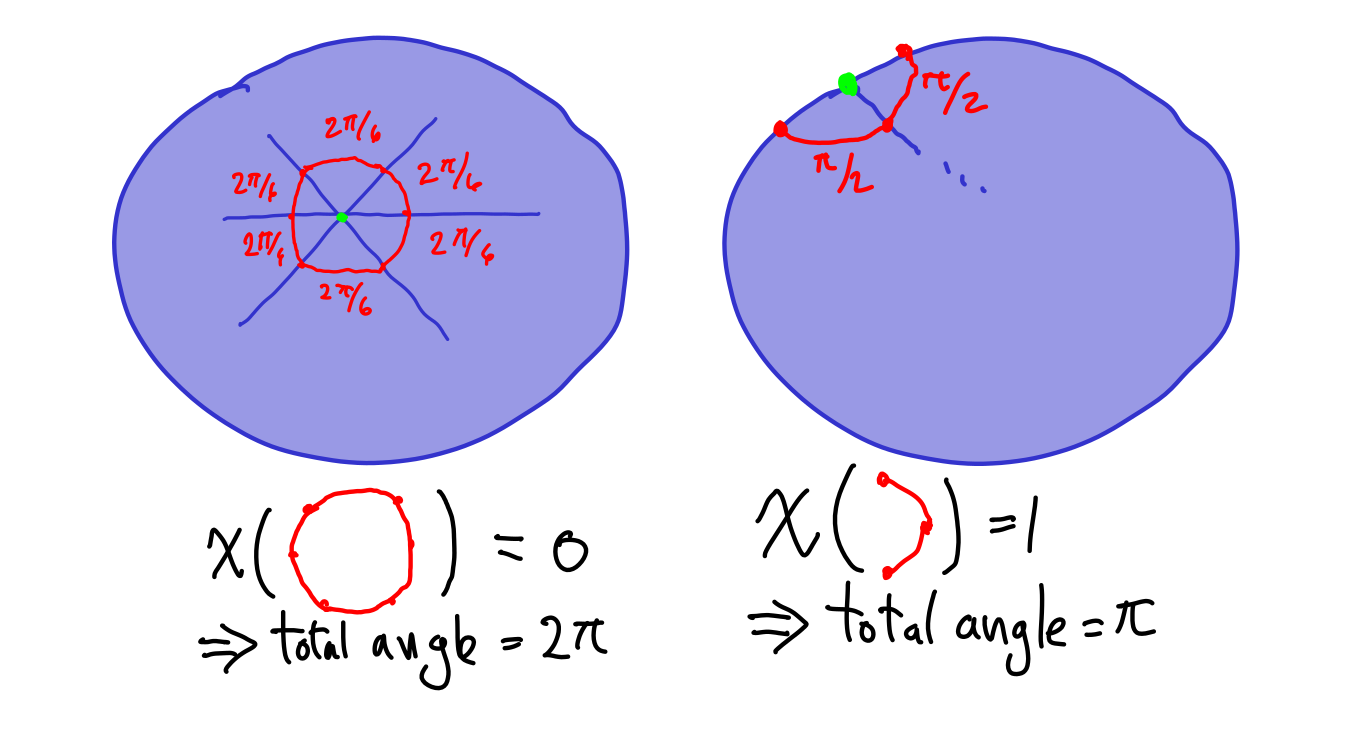
For vertices either \(v\) is interior, in which case \(\chi(\mathrm{link}(v)) = 0\) and the expected Euclidean angle sum is \(2\pi\text{,}\) or \(v\) is exterior in which case \(\chi(\mathrm{link}(v)) = 1\) and the expected Euclidean angle sum is \(\pi\text{.}\) Now if the angle sum of a vertex is equal to the expected Euclidean angle sum, then it has curvature 0. Recall the the combinatorial Gauss-Bonnet theorem holds for any angle assignment. In particular we are free to pick angle assignments which will be suitable to our purposes.

We start by assigning angles so that all vertices have curvature 0.

  • If \(v\) is interior, we set all adjacent angles to \(\frac{2\pi}{\deg(v)}\)
  • If \(v\) is exterior, we set all adjacent angles to \(\frac{\pi}{\deg(v)-1}\)
Figure 3.5.6. Assigning angles to have zero curvature interior and exterior vertices.

We note that this gives angles adjacent to interior vertices, we'll call these interior angles, a maximum possible value of \(\frac{2\pi}{3}\text{,}\) the other angles (i.e. the exterior angles) have a maximum possible angle of \(\frac{\pi}2\text{.}\)

From this it immediately follows that any internal 2-cell must have negative curvature as it must have at least seven sides and to non-negative curvature its angles must be on average at least \(\frac{5\pi}{7}>\frac{2\pi}{3}>\frac\pi 2.\)

Now \(\mathcal D\) has positive curvature overall, and this curvature comes from exterior 2-cells. Let us first consider an exterior 2-cell \(f\) that is not a shell.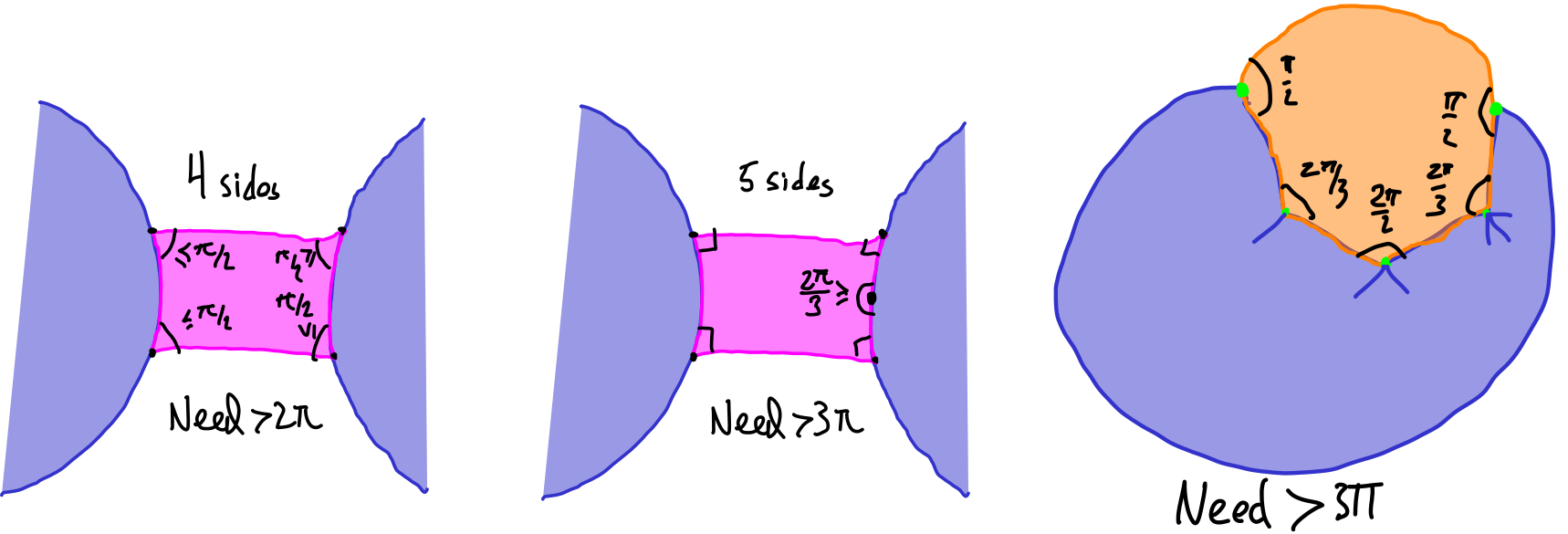

Figure 3.5.7. Exterior 2-cells which are not shells and a 4-shell

We first see that four of the corners are exterior and therefore have angle at most \(\pi/2\text{.}\) Looking at the figure, we see that a 4-sided 2 cell has curvature at most zero. A five sided 2-cell has an angle sum of at most

\begin{equation*} 4\cdot \pi/2 + 2\pi/3 = (2+2/3)\pi \lt 3\pi \end{equation*}

and therefore has negative curvature. Finally, seeing as some of the angles are at most \(\pi/2\) and none of the others can exceed \(2\pi/3\text{,}\) it is impossible to achieve even the expected Eclidean angle sum for 2-cells that have 6 or more sides, i.e. any such 2-cells will also have negative curvature.

We are therefore forced to accept that \(\mathcal D\) contains shells. Suppose finally towards a contradition that \(\mathcal D\) only contained \(i\)-shells for \(i \gt 3\text{.}\) On the one hand, if \(i>5\) then an \(i-shell\) gives rise to a 2-cell with \(i+1\) sides, and in the previous paragraph we saw that these never have positive curvature. On the other hand a 4-shell gives rise to a Pentagon with two external vertices so the maximal angle sum is

\begin{equation*} 2\cdot \frac \pi 2 + 3\cdot\frac{2\pi}{3}=3\pi \end{equation*}

and the resulting curvature is at most zero. Therefore the only 2-cells that can contribute positive curvature are \((1,2,3)\)-shells and since the total curvature is positive, these must exist.

This result immediately gives us the following corollary.

Just to be clear the reason why we chose \(1/6\) in the first place is precisely so that the bit sticking out of a \(3\)-shell is longer than the other side.

Subsection 3.5.2 Dehn's algorithm

We now present an algorithm which solves the word problem in \(c'(1/6)\) presentation.
Definition 3.5.9. Dehn's Algorithm.

Let \(w\) be some word representing an element of \(\pres X R\) consider the following algorithm for an input word \(w\text{:}\)

  1. If \(w = w' r' w''\) and \(r'r''\) is some cyclic permutation of some \(r \in R\) with \(|r''|\lt|r'|\) then repeat with \(w''=w'(r'')^{-1}w''\text{,}\) which is shorter.
  2. Otherwise, \(w\) cannot be shortened by replacing "half relations" and we stop.

Now note that at each step, the algorithm produces shorter words or terminates. Also the sequence of words it produces are all equal in the group. Furthermore, this algorithm will terminate for every word and every finite presentation. We would really like it if the algorithm reduces the word to the identity if an only if the word was trivial, or equivalently, if a word can no longer be shortened in this simplistic way that is non-trivial. But if this were the case we would have an algorithm to solve the word problem which will work for all groups, which is impossible. In fact, if we take the familiar

\begin{equation*} \ZZ^2 = \pres{a,b}{a^{-1}b^{-1}ab} \end{equation*}

and take the word \(w=aaabbba^{-1}a^{-1}a^{-1}b^{-1}b^{-1}b^{-1}\text{,}\) then we will see that Dehn's algorithm terminates on \(w,\) thus giving a "false positive" on the non-triviality of \(w\text{.}\)

That said for a \(C'(1/6)\) presentation, the presence of \(1,2,3\)-shells provide exactly the subwords of words representing the identity that can be replaces by shorter halves of relations. Now we previously only considered van Kampen diagrams which were homeomorphic to discs. More generally van Kampen diagrams are made up of discs that are either joined by vertices or graphs. We will say that a vertex \(v\) is semi-exterior if \(\mathrm{link}(v)\) is not connected. In this case either \(v\) doesn't lie in a 2-cell, or it is where some maximal disc is attached to the rest of the diagram.

Figure 3.5.10. Semi-exterior vertices

In all such cases \(\chi(\mathrm{link}(v)\geq 2\text{,}\) so in all cases the "expected" Euclidean angle sum is 0 or negative, which means that they contribute 0 or negative angles. A quick verification shows that, if anything, semi-exterior vertices make the case for \(1,2,3\)-shells even stronger and we get the general statement.

This is a quintessential combinatorial and geometric group theory result: it is an algorithmic result about group presentations which relies on the geometric notion of curvature. We also note the the failure of Dehn's algorithm on \(\ZZ^2\) can be explained by the fact that \(\ZZ^2\) is the fundamental group of the torus, which has curvature 0 and Dehn's algorithm is a negative curvature phenomenon.

Finally although algorithmic results are great we are doing algebra after all, and it would be desirable to obtain algebraic results, we have.

The simplest proof of this fact follows from using deterministic finite automata. We say that a word \(w\) is locally geodesic if it contains no subwords which are long halves of cyclic permutations of generators.

A set of words which is forbidden to contain a finite list of poison subwords forms a regular language \(L\) which can be encoded by a finite automaton \(\mathfrak A\text{.}\) It is easy to show that we can get the pumping lemma to apply and we get a sequence of geodesic words

\begin{equation*} u*(w^m)*t; m \in \mathbb N\text{.} \end{equation*}

All of these are non-trivial and it is easy to see that \(w^m, m\in \mathbb N\) is in fact a sequence of distinct \(G\)-non-trivial (in fact locally geodesic) words and the result follows.

Subsection 3.5.3 On the abundance of \(C'(1/6)\) presentations.

In this final part I want to informally explain why \(C'(1/6)\) presentations are, in a sense, abundant. First we need to define what we mean by a random presentation. We will define 4 parameters for a presentation \(\pres X,R\text{:}\)

\begin{equation*} n = |X|, m=|R|, M = \max_{r\in R}(|r|), \mu = \min_{r \in R}(|r|), \end{equation*}

i.e. the number of generators, the number of relations, the maximal generator length and the shortest generator length. We denote by \(\mathcal {P}(m,m,M,\mu)\) the set of all presentations satisfying these parameters, and it is clear that we can fix a specific alphabet \(X\) of the appropriate size so that \(\mathcal {P}(n,m,M,\mu)\) becomes a finite set.

Now if we fix \(M=1\text{,}\) i.e all relations have length 1 and we let \(m\gt\gt n\text{,}\) then with high probability every generator will show up as a relation and we'll have a trivial group. So in this random model we have trivial groups with high probability.

The few relators model random is when we fix \(n,m\) and, for example, set \(M \leq 2\mu\text{.}\) In this case, as \(\mu \to \infty\text{,}\) we'll find that the probability that a presentation selected from \(\mathcal P(n,m,2\mu,\mu)\) at random will be \(C'(1/6)\text{.}\)

To see why this is true, consider the one relator case (\(m=1\)). Failure of \(C'(1/6)\) means that there is some subword of \(r\) of length at least \(\frac{|r|}{6}\) occurs twice. To get a sense of how unlikely this is consider tossing a coin 1 000 000 times, what is the probability of the same \(16000 \approx \frac{1000000}{6}\) streak of heads and tails occurring twice? It is small. In general the probability of failure decreases exponentially as \(\mu\to \infty\text{.}\)

Now the actual argument has some technicalities involving conditional probabilities that arise, for example, from considering when subwords overlap with themselves, or shifts of cyclic words, but the situations which involve tricky technicalities only constitute a negligible portion of all possibilities and, guided by the coin-toss heuristic above, it is actually quite doable to work out an exponentially decaying upper bounds for the probability of \(C'(1/6)\) failure. In fact this will also be the case for \(C'(\lambda)\) for any \(\lambda>0\text{.}\) Basically, if the number of relations is fixed and their lengths go to infinity, you will most likely get a small cancellation presentation.

This reason alone mean that small cancellation presentations are somehow important.

Exercises 3.5.4 Exercises

1.

Let \(\pres X R\) be a \(C'(1/6)\)-presentation. Prove that it is impossible to tile a sphere 2-cells with boundary words in \(R\text{.}\)

Hint: The point of this problem is to get you to read the proof Proposition 3.5.5. Note that all 2-cells on a sphere must be"internal".

Comment: This in particular implies that \(C'(1/6)\) presentations are aspherical, which is significant when considering group cohomology.

2.

The fundamental group of a closed surface of genus 2 has the following presentation:

\begin{equation*} \pres{a,b,c,d}{aba^{-1}b^{-1}cdc^{-1}d^{-1}}. \end{equation*}

How would you go about solving the word problem for this group?

3.

In your own words, using drawings, examples, and citing results, explain why Theorem 3.5.11 is true.