Section 1.8 Solving Dehn's algorithmic problems in the class of finitely generated free groups.
We already saw that the isomorphism class of \(F(X)\) was determined by the cardinality \(n=|X|\text{,}\) so we'll fix the following notation
Solving the word problem in \(F_n\) is straightforward: bring a word to reduced form and make the obvious conlcusion.
Although the isomorphism problem is undecidable if you're working over arbitrary finite presentations. In practice we usually consider the isomorphism problem resricted to a class of groups. For finitely generated free groups we are asking whether it is possible that \(m\neq n\) but that \(F_n \approx F_m\text{.}\) We will see that the answer is "no", but before doing so a couple observations are in order.
First of all, we will see later on that for any \(m,n\) (in fact we could even take the countably infinite cardinal \(m=\aleph_0\)) there is an injective homomorphisms
In fact in the early 2000s it was proved that all finite rank free groups have the same elementary theory. All this to say that directly showing that free groups of different rank are non-isomorphic is difficult.
Given any group \(G\) we can consider the commutator subgroup
The quotient:
is called the abelianization of \(G\) and it is an abelian group since
Fans of category theory will rejoice to observe that the abelianization map is a functor from the category fo groups to the category of abelian groups.
For free groups, the abelianization is
Now if this were linear algebra we would have \(\dim(\ZZ^n)=n\) and vector spaces are isomorphic if and only if they have the same dimension. Thus
Unfortunately \(\ZZ\) isn't a field. However, there is a canonical algebraic constructions which embeds \(\ZZ^n\) into \(\QQ^n\) (or any \(\ZZ\)-module into a \(\QQ\)-vector space) is called extension of scalars and we get can use linear algebra again:
So the number \(n\) in \(F_n\) is determined by algebraic structure, and that solves the isomorphism problem.
Actually there is a name for this group invariant.
Definition 1.8.1.
Let \(G\) be a finitely generated group then \(b_1(G)\text{,}\) the first Betti number of \(G\) is the torsion-free rank of the the abelianization \(G/[G,G]\text{,}\) viewed as a \(\ZZ\)-module or
Let's now tackle the conjugacy problem. A useful tool for free groups is cancellation diagrams. Note that for the remainder of the section we will sometimes put a \(\cdot\) to denote multiplication for emphasis. Let \(w_1\) and \(w_2\) be reduced words then we have the cancellation diagram: 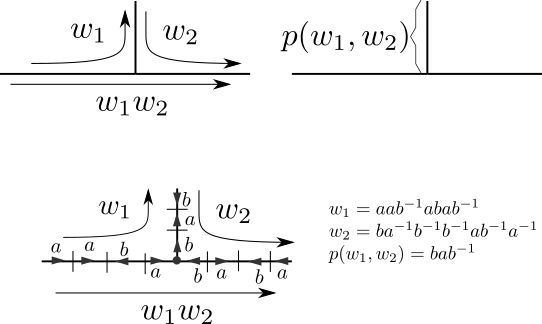
And we denote by \(p(w_1,w_2)\) the maximal co-terminal subword of \(w_1\) that cancels in the product \(w_1\cdot w_2\text{.}\) We will call this the pinch in the product \(w_1\cdot w_2\text{.}\)
When conjugating \(u^{-1}\cdot w \cdot u\) we can obtain different combinatorial types of cancellation diagrams. 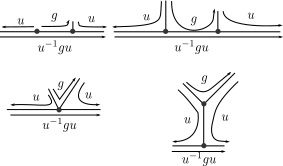
Let's now solve the conjugacy problem. The conjugacy class of \(w\) consists of the set \(\{g^{-1}w g \mid g \in G\}\text{.}\) Given a reduced word \(w \in F_n\text{,}\) there is an algorithm to find a word \(u\) such that \(uwu^{-1}\) is cyclically reduced.
Definition 1.8.4.
A reduced word \(w=x_1\cdots x_{m} \in F_n\text{,}\) \(x_i \in
\{a_1,\ldots,a_n\}^{\pm 1}\) is cyclically reduced if \(x_1 \neq x_m^{-1}.\)
Lemma 1.8.5.
Lemma 1.8.6.
In \(F_n\text{,}\) a cyclically reduced word has minimal length within its conjugacy class.
Lemma 1.8.7.
Given any cyclically reduced word \(w=x_1\cdots x_{m} \in
F_n\text{,}\)
Corollary 1.8.8.
The conjugacy problem in \(F_n\) is solvable.Proof.
Exercises 1.8.1 Exercises
1.
Let \(G = \pres{a,b,c}{aa,abc,bab^{-1}a^{-1}}\text{.}\) Compute \(b_1(G)\text{.}\)
Hint: Work in abelianizations. Let \(a,b,c\) be the vectors \(\BEmatrix{1\\0\\1},\BEmatrix{0\\1\\0},\BEmatrix{0\\0\\1}\) respectively. The relations also correspond to vectors, e.g. \(abc=\BEmatrix{1\\1\\1}\text{.}\) Now \(G/[G,G]\otimes_\ZZ\QQ\) is the vector space
where \(U\) is the subspace spanned by the relation vectors, and \(\dim(V)=3-\dim(U)\text{.}\)
2.
Consider this more elementary approach to showing that \(b_1(G)\) is a group invariant. If \(G = \pres X R\) is a finite presentation, assign to each \(x_i \in X\) the standard basis vector \(e_i \in \QQ^{|X|}\) and for each \(r \in R\) take the vector \(v_r \in \QQ^{|X|}\) to be the vector whose \(i\)th entry is the sum of the exponents of the letter \(x_i\text{.}\) Let \(U = \mathrm{span}\{v_r \mid r\in R\}.\)
Show that for every elementary Tietze transformation, although you change the presentation the number
remains unchanged.
Explain why this impies that \(b_1(G)\text{,}\) as calculated in the previous problem, depends on the group \(G\) and not on some particular choice of presentation.
3.
Prove Lemma 1.8.5
4.
Prove Lemma 1.8.6
5.
Prove Lemma 1.8.7
